Why Johnny Can't Add - Chapter 5: Rigor.

Chapter 5: Rigor.

Geometry is nothing if it be not rigorous, . .
The methods of Euclid are, by almost universal
consent, unexceptionable in point of rigour.
Henry John Stephen Smith (1873)

The modern mathematics leaders are not content with a deductive approach to mathematics. They wish to present a rigorous deductive development.

Let us first be clear as to the distinction between a deductive development and a rigorous deductive develop-inent. Euclidean geometry as most adults learned it in high school, which is essentially Euclid's own presentation in his Elements of about 300 B.C., is deductive. However, it is not rigorous. The distinction lies in the fact that Euclid and his successors up to recent times used implicitly axioms and theorems that are so obviously true that they either did not realize they were using them (just as we are usually unaware of breathing air) or they thought there was no need to assert them or mention them in proofs. Thus, it is obvious that a line divides a plane into two parts and that a triangle has an inside and an ontside. If we have three points on a line it seems abundantly clear that one and only one of these three points lies between the other two.

Or consider another example. Suppose two circles are drawn with the distance between the two centers less than the sum of the two radii (Fig. p63). Euclid did not hesitate to affirm that the two circles intersect in two points. This fact is not guaranteed by Euclids axioms. One could argue that the structure of the circle might be such that just at the two places where the circles are presumed to intersect either circle or both may fail to have points on them. The argument is technically correct. However, Euclid's concept of the circle, like our intuitive concept, was what one might describe as a continuous structure, that is, one with points everywhere along the circumference.

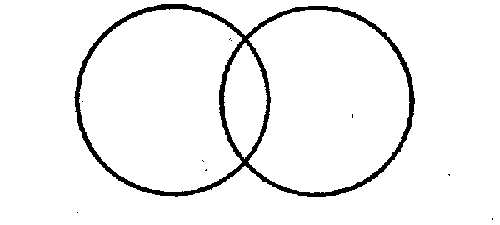
Fig. p63

As we have stated, the above described facts and others were used by Euclid and the traditional texts without mentioning them explicitly. The modernists believe that students are disturbed by the use of unmentioned assumptions and theorems and that, because the proofs -are not strictly complete, the students are hindered in their understanding. It is also deceitful, say the modernists, to present proofs that are purportedly complete but are not actually so.

The remedy for these "defects" in traditional Euclidean geometry is to supply additional axioms and then to prove every assertion, no matter how obvious, by deductive reasoning. The new axioms are of several types, axioms of existence, axioms of order, and a continuity axiom. Among the axioms that must be added are the assertions that the line joining any two points is unique, that the distance between two points is unique, that a plane contains at least three points, and that a line divides the plane into two parts. There is also a continuity axiom which in effect guarantees that the two circles previously described meet in two points and that if A and B (Fig. p64 are on opposite sides of a line l, the line joining A and B actually intersects l in a point common to the two lines. The wording of these additional axioms varies somewhat from one modem text to another.

Fig. p64

All the axioms and theorems required for a rigorous deductive approach to geometry are spelled out in mod-ern mathematics treatments. This involves many addi-tional axioms and dozens of theorems in which the results are intuitively obvious. For example, one proves that a line segment not only has a midpoint but a unique midpoint, and that a triangle has an inside and an outside.

In algebra, too, rigor is incorporated. Thus, one does not presuppose that the result of adding 4 and 6 is a unique number. Conceivably there could be two answers.

One adopts what is called a closure axiom which asserts the existence and uniqueness of the sum. In dealing with the relation of equality one does not take for granted its obvious properties. One adopts as an axiom that a = a and this property is called reflexiveness. Can one be certain that if a = b then b = a. An axiom assures us that it is so. This property is called symmetry. Finally, one postulates that if a = b and b = c, then a = c, and thus the transitivity of equality is assured.

It is true in algebra as in geometry that the edition of the many axioms which rigor demands requires that a number of obvious theorems be proved, even though students would otherwise use these theorems without recognizing that they had called upon them.

Is the incorporation of rigor a contribution to pedagogy? Let us note first of all that some of the defects now recognized in Euclid's development of geometry are readily remedied. Thus, Euclid's method of establishing various theorems on the congruence of triangles rests on his axiom that two figures are congruent if they can be superposed. There are valid objections to this axiom but the objections are easily met by introducing instead an intuitively acceptable replacement, namely, that two triangles are congruent if two sides and the included angle of one triangle are equal to two sides and the in-cluded angle of the other. In this instance the improvement on Euclid does not involve subtleties that are beyond the understanding of young people; hence, there is no reason not to make the change. However, there are serious objections to supplying most of the axioms and theorems that a truly rigorous deductive development requires.

Until about one hundred years ago mathematicians regarded Euclid's presentation as the model of rigor.

It is true that occasionally a mathematician wòuld either criticize the wording of an axiom or point out the need for an additional axiom. But no one took these criticisms seriously because they called for no more than minor changes or additions. It was the creation of non-Euclidean geometry in the first third of the nineteenth century which forced matheniaticians to be more critical of what they had accepted in Euclidean geometry, and therewith they became aware that Euclid had used many axioms and theorems which are intuitively so obvious that he was not aware he was using them.

To ask students to recognize the need for these missing axioms and theorem is to ask for a critical attitude and maturity of mind that is entirely beyond young people. If the best mathematicians did not recognize the need for these axioms and theorems for over two thousand years how can we expect young people to see the need for them? That for two thousand years Euclidean geometry, as formulated by the presumably careless or naive Euclid, was regarded by the best mathematicians as the para-digm of rigor bears no weight with the advocates of rig-orous axiomatics. Today's students, we are apparently supposed to believe, are sharper and ase not satisfied with the cruder version presented by Euclid. Presumably, this too is a reason that they do not do well in geometry.

In presenting rigorous developments of the number system and of geometry we first have to make sure that students appreciate the gaps that rigor meets and then teach the rigor. Thus, in the case of geometry students use figures which automatically take care of such details as the order of points on a line, but which the rigorous presentation covers through suitable axioms. Hence, the teacher has to spend a great deal of time in making a student realize that he has accepted many facts on an intuitive or visual basis. Even if sufficient emphasis and persistence on the part of the teacher make students see the need for the missing axioms and theorems, they will draw a conclusion that will hardly endear mathematics to them. In a rigorous development of geometry and algebra many intuitively obvious theorems must be proved. The students' conclusion will be that mathematics is largely concerned with proving the obvious.

Further, the axioms that mathematicians adopt in a rigorous approach, though simple in the sense that they deal with basic properties of points, lines, and planes, are not obvious properties that one would naturally adopt. For example, one of the order axioms specifies that, given any three points on a line, one and only one lies between the other two. Another specifies that a line which cuts one side of a triangle necessarily cuts another side. Still another specifies that if the points of a line are divided into two sets such that all the points of one set precede, in the order of the points on a line, all those of the second set, then there is one and only one point which separates the points of the two sets. Such axioms are introduced to prove the simplest theorems of Euclidean geometry. In fact, many of the theorems are more obvious than the axioms used to establish them. Hence, the less obvious is used to prove the more obvious. But as far as the student is concerned the whole point of proof is just the reverse. Students will question what is being accqmplished and perhaps even wonder whether teachers are sane.

Henri Poincaré, in an article on logic and intuition, struck at this folly. "When a student commences seriously to study mathematics, he believes he knows what a fraction is, what continuity is, and what the area of a curved surface is; he considers as evident, for example, that a continuous function cannot change its sign without vanishing. If, without any preparation, you say to him: No, that is not at all evident; I must demonstrate it to you; and if the demonstration rests on premises which do not appear to him more evident than the conclusion, what would this unfortunate student think? He wlll think that the science of mathematics is only an arbitrary accumulation of useless subtleties; either he will be disgusted with it or he will amuse himself with it as a game and arrive at a state of mind analogous to that of the Greek sophists."

Almost three hundred years earlier Blaise Pascal said in his Pensées, "Never undertake to prove things that are so evident in themselves that one has nothing clearer by which to prove them."

Another consequence of incorporating all of the axioms a rigorous approach to Euclidean geometry requires is that a host of trivial theorems must be proved before the significant ones are reached. The number of minor theorems is so large that the major features of the subject fail to stand out. Moreover, the time consumed in proving the obvious theorems deprives the students of the time to study significant, deep theorems that are essential to progress in mathematics.

The rigorous development of a branch of mathematics is often so artificial that it is meaningless. No example is more pertinent than the logical development of the real number system. There were good reasons to axiomatize the number system, but the introduction of fractions and negative numbers as couples (see Chapter 4) with special definitions of the operations with these couples, clever as it may be, is so artificia1, trumped-up and foreign to the intuitive meaning and uses of these numbers as to preclude understanding.

Many teachers might retort that the student has already learned the intuitive facts about the number system and is now ready for the appreciation of the rigorous version, which exemplifies mathematics. If the student really understands the number systern intuitively, the logical development will not only not eithance his understanding but will destroy it. As an example of mathematical rigor no poorer choice could be made because the construction is so contrived. The development. is so full of details and so stilted that it not on1y stultifies the mind but obscures the real ideas. Yet just this topic has now become the chief one in high school and college mathematics courses.

Some of the axioms used in a rigorous approach to the rea1 number system must strike the students as absurd. They are asked to accept the closure axiom. In the case of the integers, for example, this reads: The sum of two integers is an integer. Were the students not properly forewarned by this axiom would they have thought that the sum of two integers is a cow? In the case of the rational numbers (positive and negative whole numbers and fractions) the uniqueness of inverses to addition and multiplication is stressed. Would the students have ex-pected two answers for subtraction or two for division? These closure axioms may serve one purpose: they close the gates of the students' minds.

The distinction between deductive proof and rigor involves a further complication. Rigorous proof is not static. The demands of rigor are constantly changing and increasing in complexity. Mathematics grows like a tree. As the trunk, branches, and leaves increase, the roots go deeper. It is safe to say that no proof given at least up to 1800 in any area of mathematics, except possibly in the theory of numbers, would be regarded as satisfactory by the standards of 1900. The standards of 1900 are not acceptable today. Hence, the pedagogical significance of the constantly increasing standards of rigor is that if the texts continue to keep up with them the students will constantly be burrowing further down to the roots and will never get to see the tree proper. However, it is not necessary to pursue this rigor. Young people will not see the need for it any more than did the great mathematicians of a hundred years ago. What was intuitively acceptable two thousand years ago is still intuitively acceptable today. Moreover, the students can be much more readily attracted to the fruits rather than to the roots of mathematics.

It is rather ironic that the reformers, in their efforts to be modern and up-to-date, decided to emphasize the rigor of 1900. They are at least seventy-five years too late. As the finishing touches were being put on the rigorous approaches that appeared satisfactory at the end of the nineteenth century, difficulties in the logic of mathematics were uncovered in just that branch of mathematics, set theory, which is the most heavily emphasized topic of the new mathematics. The difficulties, which are euphemistically called the paradoxes of set theory, but which are more accurately described as contradictions in set theory, have not been resolved to the satisfaction of all mathematicians, and the logic öf mathematics has never been in a sorrier state. Indeed, there is no agreement at all today on what constitutes a correct mathematical proof, and it is fairly certain that an axiomatic approach to any branch of mathematics cannot be adequate.

We cannot enter here upon the history of rigor or upon the difficulties in building mathematics rigorously, but we can state that many mathematicians are sufficiently skeptical of whether we shall ever attain rigor to make sarcastic remarks such as "Logic is the art of going wrong with confidence"; . . . "The virtue of a logical p Color roof is not that it compels belief but that it suggest doubts . . ."; "A mathematical proof tells us where to concentrate our doubts."The whole attempt to inject rigor in mathematics has amounted to picking up jewels ouly to discover serpents underneath.

Like deductive reasoning, rigor does play a role in mathematics, but it is the concern only of professional mathematicians who wish to ensure that the deductive structures are sound. Such men, who have developed a critical spirit after years of specialization, can see the need for rigor and appreciate what it supplies. Without that experience, the detailed and sophisticated axiomatics appear to be senseless, futile inventions. Hence, to offer it to young students is to bewilder and baffle rather than to aid them. In fact, the rigorous deductive presentations introduced by the great mathematicians of the late nine-teenth century and the early part of this century were never intended as an aid to pedagogy. The great mathe maticians who have taken an interest in pedagogy always stressed that strict logical presentations are entirely subordinate to the substance, which is learned intuitively.Rigor may save mathematics but it will surely lose the pupils.

In view of the detriments to pedagogy which rigorous presentations impose, one might well ask why the curriculum-makers incorporated it. We have 4pointed out that the many curricula were written by groups of mathematicians and teachers drawn from all levels of the mathematical world. Some of these writers, oniy recently informed of the rigor of 1900, became enthusiastic about presenting what they thought was the new face of mathematics. Of course, they confused what is logically prior with what is pedagogically desirable. Others seeking novelty fastened on rigor. Among the many writers were shallow, relatively ignorant mathematicians who took th simple topics of elementary mathematics and made them appear profound by cloaking them in what for young people can be described on1y as prissy pedantry. They sought thereby to give the impression of deep mathe matical insight. It is easier to incorporate sophistication in trivial matters than to give clear intuitive presentations of the more difficult ideas. Certainly much of the rigor in modern texts was inserted by limited men who sought to conceal their own shallowness by a facade of pro furidity and by pedants who masked their pedantry under the guise of rigor. One can rightly accuse thein of pseudo-sophistication. If mathematical education of the traditional type has suffered from the martinets who imposed rote learning, the newer education will suffer more borribly from the rigor-mongers.

Chapter 6: The Language of Mathematics

If youre anxious for to shine in the high aesthetic line as a man of culture rare,
You must get up all the germs of the transcendental terms, and plant them everywhere.
You must lie upon the daisies and discourse in novel phrases of your complicated state of mind, The meaning doesnt matter if its only idle chatter of a transcendental kind.

And every one wilI say
As you walk your mystic way,

"If this young man expresses himself in terms too deep for me, Why, what a very singularly deep young man this deep young man must be!"

Sir W. S. Gilbert

One of the defects of the traditional curriculum, according to the modern mathematics leaders, is its imprecise language. The looseness and ambiguities are supposedly so numerous and so deplorable that students are seriously handicapped. The new curriculuin claims to eradicate these defects by introducing precise language. Let us see how serious the defects have been and how they are purportedly eliminated.

To illustrate the inaccuracy of the traditional language, the modernists give the following illustrations. "Peter bas four balloons and Joe has five balloons. How many balloons do both have?" Almost everyone would understand the language to mean, "What is the sum of the number of balloons Peter has and the number Joe has?" and would answer nine. Not so, say the modernists. Both boys do not have any balloons, and they mean of course that they have no balloons in common.

A second illustration states, Mary spent twelve cents for two pencils"; then it asks, "How much did she spend for each?" Most people would answer six cents because they would assume, in the absence of further information, that the two pencils are alike. The modernists object. There was no explicit statement to the effect that the pencils were alike.

Clearly these questions, if indeed imprecisely worded, could certainly be restated without requiring any special language. But the modernists believe that a drastic improvement in the Ianguage of mathematics is called for.

To secure precision they make the distinction between number and numeral. The symbol 7 is not a number but a symbol for a number. Other symbols for the same number are 3 + 4, 5 + 2, 8-1, and many more. Students are expected to learn that they deal with numerals rather than numbers. To point up the necessity for the distinction the modern texts give the following example. One can say that the number 343 contains three digits. But 343 = 7³,Hence, one should be able to say that 7³, which is the same number, contains three digits. The original statement should have been that the numeral 343 contains three digits.

Apropos of the distinction between number and numeral there is a story that one writing group entitled a chapter. "Learning to Read and Write Large Nutnbers". When the group was apprised that one reads and writes numerals rather than numbers, they changed the word "numbers" to "numera1s". But this title, they soon realized, could mean writing large-sized numerals and so the title was further changed to "Learning to Read and Write Numera1s for Large Numbers". By this time no one un-derstood what was meant.

Precision of language is further "insured" by using the. language of sets. Sets are no more than collections of objects, for example, the set of all apples, the set of whole numbers, and the set of men. By using the concept of a set one can rephrase and presumably make precise many mathematica1 statements. Thus, instead of asking for the values of x that satisfy x + 3 = 5, one calls such expressions open sentences and asks for the tmth set of this open sentence. The truth set means the va1ues of x which. make the equation correct. Of course, there is only the value x = 2. in the truth set of this open sentence. The truth set of the open sentence x² = 4 consists of 2 and -2.

To secure precision the modernists have replaced many definitions in the traditional texts with their own versions. In a traditional text a variable might be defined. as a symbol or letter which can take on any one of some collection or set of va1ues. Thus the x in y = x²can be assigned any real number. This language is not acceptable in modern mathematics. Instead, a modern text says that a variable is a symbol which may represent any of the elements of a specified set. A set whose elements serve as replacements for a variable is called the rep1acement set for the variable. This set is also called the domain of the variable. The individual members of the replacement. set are called the values of the variable. A variable with just one va1ue is called a constant.*

*Logically this definition of a variable seems troublesome. If a constant must be defined as a variable with just one va1ue, then what are the elements of the replacement set? Are they not constants? If so, the concept of constant is already involved in the definition of a variable.

Variables are important because they enter into functions. Thus y = x² is a function, and the traditional definition of a function is a relationship between variables such that if a value is assigned to one variable the value or va1ues of the second one are determined. Thus, in the case of y = x², if x = 3 then y has the single value of 9. On the other hand, if the function is y² = x + 5, then when x = 4, y = +3 and y = -3. The function y = x² is said to be single-valued and the function y² = x + 5 is said to be multiple-valued.

Such "sloppiness" is not permitted in the modern texts. They first introduce the notion of an ordered pair. Thus (3,4), (5,6) and (6, -2) are ordered pairs of real numbers. The concept of function, single- or multiple-valued, is replaced by the concept of a relation. A relation is any set of ordered pairs. A function (meaning single-valued function) is a relation in which no two different ordered pairs have the same first number. Thus, (4,3) and (4, -3) could not belong to the set of ordered pairs which define a function. Given these definitions of relation and function, the students are expected to see that y² = x + 5 is a relation and y = x² is a function.

Precision is secured in geometry by carefully distinguishing concepts. An angle, for Euclid, is the inclination to one another of two lines which meet. Apparently this wilI not do. An angle now is the figure formed by two rays (half-lines) that meet in a common point O (Fig. p77). Of course, if an angle is just the two rays we do know which angle is referred to, augle A or angle B. To decide we need to know what the interior of an angle is. For this purpose we call upon another axiom (or theorem in some developments). This axiom states that a

Fig p77

line divides the plane into two parts. Hence, if we take the part determined by the line OC (which contains the ray OC) and contaíning D and take the part determined by the line OD and containing C and now take the set intersection of these two parts (the points comxnon to these two parts) we obtain the interior of the angle DOC. Having determined the interior of the angle we can prove that if E axid F are in the interior of an angle (Fig. p77), then the segment EF lies in the interior of the angle.

Knowing which angle we have in mind does not tell us what the measure (size) of the angle is. For this purpose another axiom tells us in effect that to all rays emanating from O (Fig. p77) and beginning with OC numbers can be assìgned and the number assigned to OD is the meas~ ure of angle DOC. Thus to OC the number 0 is assigned because the numbering starts with it and to OD the number 30 might be assigned. Then the size of angle COD is 30.

Angles are often studied as parts of triangles. We might be tempted to say in looking at Figure fig. p78 that angle A is an angle of triangle BAC and that BA and CA are the sides of angle A. This would be grossly incorrect. The sides of an ang1e are rays which extend to inflnity, whereas BA and CA are finite segments. However, some authors grant dispensation to favored readers and permit them to speak of angle A as an angle of triangle BAC.

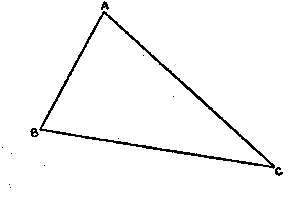
Fig. p78

Euclid was careless in defining a triangle as a figure formed by three line segments. Of course this will not do. Figure Fig. p79-1 is formed by three segments and is not a triangle. Properly, a triangle is the figure consisting of the union (a set theoretical notion) of three noncollinear points and the line segments joining these points.

In elementary algebra and again in coordinate or analytic geometry students learn what a rectangular coordinate system is. In this system each point of the plane is located by two numbers. The first is the distance of the point to the right or left of the y-axis and the second is the distance above or below the x-axis. Thus the coordinates of P in Figure 79-2 are 2 and 4. These are written as the ordered pair (2,4). This approach to coordinates

Fig. p79-1

is too crude for many modernists. They approach the notion of a coordinate system through the concept of a product space. If one has two sets A and B then the product space consists of all pairs (a,b) where a belongs to A and b belongs to B. The order of the elements inthe pair must be preserved. That is, the product of A and B is not the same as the product of B and A. To arrive at the notion of coordinates for points in the plane, A and

Fig. 79-2

B are each taken to be the set of all real numbers and the product space of these two sets is the set of coordinates (a,b). Then a is identified with the distance of P from the y-axis and b with the distance of P from the x-axis. The notion of product space is supposed to introduce precision in the deflnition of coordinates.

In keeping with their aim to secure precision, the modern texts define carefully every concept that is used. The consequence is an immense amount of terminology. Thas one finds definitions for angle, triangle, polygon, numeral, equation, open phrase, open sentence, compound sentence, algebraic expression, binary operation, closure, inverse, uniqueness of inverse, null set, union, intersection, solution set, line segment, point pair, distance, length, ray and many other terms. An actual count of the number of terms introduced in the ninth-grade algebra course and tenth-grade geometry course shows that several hundred terms are introduced in each one. Of course, students are expected to learn and use these terms.

Much of the terminology is abstract. The authors of the modern texts naturally wish to introduce addition and multiplication. These operations applied to numbers are taught in the elementary grades. Applied to letters they are taught in algebra. However, the terms addition and multiplication are considered too mundane. To treat adding 5 and 7, the texts speak of a binary operation, meaning that addition applies to two numbers or letters. Multiplication, likewise, is a binary operation.

These examples may illustrate what the modernists mean when they say that errors and fuzzy thinking can be eliminated by precise language. Now we'll consider their claim. Typical of the precision is the distinction we have already noted, namely, the distinction between a number and a numeral. The distinction raises a question. If 7 is a numeral for the number seven, what is the number? This, the students are told, is an idea in their minds. The answer is hardly satisfying to young people and the distinctìon has done more harm than good. It has shrouded number in mystery and made students more dubious of their capacity to understand.

Of course, there is a distinction between number and numeral, and between Robert Smith, the name, and Robert Smith, the boy. However, language incorporates practices that may cut corners but nevertheless promote effective communication. Excess verbiage is to be avoided if there is no danger of error. It would seem unnecessary to say the boy whose name is Robert Smith when saying Robert Sinith clearly refers to the boy and not to his name. Context determines meaning in almost all cases. The 2 in 245 and in 425 have difierent meanings; yet no confusion is incurred.

Much of the new terminology is totally unnecessary. To speak of binary operations, closure, and many, many other terms labels what need not be labeled. Some terminology replaces older terminology but to no partìcular advantage. Thus x + 2 had been called an expression. It is now an open phrase, open because the. value of x is not specified. An equation, say, x + 2 = 0, will presumably become clearer if it is renamed an open sentence. The problem of solving an equation in x becomes the problem of finding the truth set of an open sentence, but the job of solving an equation remains precisely what it was before the new terminology was introduced.

The common understandings which students have acquired through experience are good enough; formal definitions are not usually needed. Students know what a triangle is and do not have to be taught that it consists of the union of three noncollinear points and the Iine segments joining them. After reading such a definition one must think long and hard to realize that it defines the familiar triangle.

The terms "relation" and "function" have replaced multiple-valued and single-valued functions. The older term, multiple-valued function, was meaningful; the newer one, relation, is vague. Beyond this, relation and function are defined in terms of sets of ordered pairs. Such a set is supposed to convey the idea of, say, y = 3x, wherein x can take on all reaI numbers as values and y is three times x. However, the function has an infinite number of x and y va1ues. The definition as a set of ordered pairs gives a distorted view because it gives the impression that the number of pairs in the set is finite. Further, the function cannot be specified by enumerating the set of ordered pairs because the number of these is infinite whereas y = 3x does convey the entire function. Finally, the basic intuitive idea of a function - that is, as the values of one variable, x, change, the values of the second variable, y, are dependent on the va1ues of the first one and change with it - is lost in the static description of a set of ordered pairs. Apparently novelty is desirable even at the cost of understanding.

It is only fair to admit that there are functions wherein x may take on only a finite number of integraI values. For example, the function describing the population of, say, New York City, wherein x is the time, say the number of months from January 1, 1950, to January 1, 1970, and y the corresponding population, will have on1y a finite number of integral va1ues for x and for y. Though the ordered pair definition is more applicable in these special cases, it is not helpful.

The introduction of so many new terms, and particu larly terms which are not suggestive of the concepts they represent, puts an intolerable burden on the memory.

The excessive terminology has been criticized by Richard P. Feynman. professor of physics at the Califofnia Institute of Technology, and a Nobel prize winner in 1965. Professor Feynman served as a member of the California State Curriculum Commission which examined texts, to be used in the California schools. In his article "New Textbooks for the New Mathematics, which appeared. in Engineering and Science, he attacked the excessive terminology introduced in geometry.

"Some of the books go a long way with the definition of a closed curve, open curve, closed regions, and open regions and so on, . . and yet they teach no more geometry than the fact that a straight line drawn in the plane divides the plane into two pieces. At the end of some of these geometry books, look over to find, at the end of a long discourse, or a long effort at learning, just what knowledge of geometry has been acquired. I think that often the total number of facts that are learned is quite small, while the tota1 number of words is very great. This is unsatisfactory. Furthermore, there is a tendency in some of the books to use most peculiar words -the words that are used in the most technical jargon of the pure mathematician. I see no reason for this."

Terminology, particularly pretentious terminology, is no substitute for substance. In view of the emphasis on terminology the reformers evidently believe that giving names to things automatically confers power over them. Many critics have charged that the modern mathematics texts are no more than dictionaries or studies in linguistics.

There is little doubt that the newness attributed to the new mathematics results largely from the introduction of a new terminology which serves less well than the older one. What has been brought into modern mathematics is not so much modern mathematics as the verbiage and sometimes the parody of it.

Another aid to precision heavily exploited by the new mathematics is symbolism. Since sets are a basic idea in this curriculum, there is. a notation for them. Thus { 1 ,2,3} denotes the set containing the objects 1, 2 and 3.

This curriculum also distinguishes between an object and the set which consists of that object. Thus 3 and { 3 } are different entities. The reason for the distinction is that the set (3} can be added to other sets, but the object 3 cannot be added to other sets, just as horses and cows cannot be added unless we think of them as belonging to a higher genus of animals. Whether the students appreciate this distinction is open to question; but if they do, the next point is likely to upset them. In the theory of sets the concept of an empty set enters. The empty set, commonly denoted by the Greek Ø, is illustrated by the set of all kings of the United States. However, the set consisting of the ernpty set, namely (Ø}, is not empty be-cause it contains the empty set. *

*Thus we can build something out of nothing and rise from rags to riches

The criticisms that apply to terminology apply equally to the use of symbols. It is of course granted that some symbolism is usefu1 and even necessary. Well-motivated and suitably chosen notation contributes to the clarification of essentia1 mathematica1 concepts and relations and saves labor in operations. It also aids in the understanding of ideas. To say in words what the expression a² + 2ab + b² states would not only require more length but would make comprehension difficult.

However, in the excessive use of symbols the modern mathematics curriculum has made a vice out of a virtue. Consider the following-:

- where N means the set of all integers. All this symbolism amounts to the statement, Determine all the integral solutions of 3x - 2y = 1. The modern authors are symbol-happy. Thus we find braces, brackets, vertical bars, parentheses, quantifiers, cup and cap, the one-way implication symbol and the two-way implication symbol, for belongs to, and many other symbols. Students are stunned by dark forbidding symbols.

Many symbols serve almost no purpose; the English language is better. The slight saving in space is more than offset by the psychologica1 handicap that symbolism imposes on the students. To wallow in symbols is to make reading and comprehension more difficult. When the burden of remembering what the symbols stand for becomes great, more harm is done than by using verbal statements. Moreover, symbols frighten students and so should be used sparingly. The difficulty in remembering the meanings and the genera1 unattractiveness of symbolic expressions repel and disturb students; the symbols are like hostile standards floating over a seemingly impregnable citadel. The very fact that symbolism entered mathematics to any signiflcant extent as late as the sixteenth and seventeenth centuries indicates that it does not come readily to people.

Symbolism can serve three purposes. It can communicate ideas effectively; it can conceal ideas; and it can concea1 the absence of ideas. It often seems as though the modern mathematics texts use symbolism to conceal the poverty of ideas. Alternatively the purpose of their symbolism seems to be to make the obvious inscrutable and so repel the understanding.

The inordinate emphasis on symbolism would give most people an impression of mathematics analogous to that derived from a presentation of music which puts the total effort to learning to write and read musica1 notation. No inkling would be given of what the notes, sharps, flats, the beats in a measure or any other symbols mean in terms of actual sounds, beautiful themes and complete compositions which the symbols merely record. Indeed, the analogy between mathematics and music, so far as education is concerned, extends even further. No one writes out the notes of a musica1 composition and then plays it to see what the notes call for. The ideas and even the entire development are envisioned and "played" in the composers mind before he records them in the musical notation.. So too the ideas and the arguments with which the mathematician is concerned have physical, intuitive or geometrica1 reality long before they are recorded in the symbolism. One sees then that the symbols of mathematics, like the notes of music, are in themselves merely an artificial, intrinsically meaningless script. They will convey life, meaning, richness of thought and beauty only if the ideas and the thinking which the symbols merely record are taught with as little use of symbolism as possible.

Despite the disadvantages in the use of symbols, the modern mathematics texts prefer to use them generously. One suspects that they do so to give an air of profundity to simple and straightforward material. One even finds verbal statements "elucidated by symbolic expressions", as though symbols clarify words.

The ridiculousness of the efforts to secure precision through terminology and symbolism has been attacked by Professor Feynman. In his article New Textbooks for the New Matheinatics, he criticised the precision sought by using set language. He mimics the precision by pointing out, "A zookeeper, instructing his assistant to take the sick lizards out of the cage, could say, 'Take that set of animals which is the intersection of the set of lizards with the set of sick animals out of the cage.' This language is correct, precise, set theoretical language, but it says no more than 'Take the sick lizards out of the cage'. . . . People who use mathematics in science, engineering, and so on, never use the long sentences of our imaginary zookeeper. . . . It will perhaps surprise most people who have studied these textbooks to discover that the symbol representing union and intersection of sets and the special use of brackets and so forth, all the elaborate notation for sets that is given in these books, almost never appear in any writings in theoretical physics, in engineering, in business arithmetic, computer design, or other places where mathematics is being used. I see no need or reason for all this to be explained or to be taught in school. It is not a useful way to express one's self. It is not a cogent and simple way. It is claimed to be precise, but precise for what purpose?"

Feynman includes in his critique these words: "Many of the math books that are suggested now are full of such nonsense - of carefully and precisely defined special words that are used by pure mathematicians in their most subtle and difficult analyses, and are used by no-body else. . . The real problem in speech is not precise language. The problem is clear language." He gives as an example a now common form of attempted precision, the distinction between the picture of a ball and a ball. A text says, "Color the picture of the ball red" instead of "Color the ball red." Feynman points out that the phraseology "Color the picture of the ball red" begins to produce doubts, whereas "Color the baIl red" would not.The picture of the ball includes the ball and a background. Should one color the entire background too? As Feynman also indicates, the material on sets, now given heavy play, is used only by forcing it into artificial and complicated constructions.

Back to Contents

Version 30th March 2018

[HomePage] Prof Morris Kline