|
Introducing vectors John Roche
During many years of teaching vectors to sixth-formers and undergraduates I felt, perhaps more than in any other topic of physics, that I was teaching manipulation rather than understanding. The better students grasp vectors intuitively but the weaker students - or even those bright students who demand to understand physics - are often mystified. Vector graphics is easier to teach than vector algebra, but there are difficulties with both. Early in my career I had the good fortune to encounter a student who told me that he had understood Ohm's law until I explained it. I learned then that subtle explanations must be avoided. With difficult subjects we also need to phrase our explanations very carefully, and pace them well - otherwise they may crash in the minds of our students! Clear explanation is, of course, insufficient. Different teachers use different classroom aids and approaches. My own favoured way of promoting active learning is to develop as much of the subject as possible through challenging questions addressed to the class. The teaching of vectors provides the opportunity to illustrate
several important strategies used by the physicist such as simplification, the role of fictional entities, the
fertility of the geometrical representation of non-geometrical quantities and the usefulness of geometrical algorithms. Vector graphics is more than 2000 years old. It was originally used to compound velocities. Vector algebra is a little more than a century old: it grew out of fragments of William Rowan Hamilton's quaternion notation, which had a strong geometrical interpretation. Many physicists late last century searched through various branches of physics looking for physical applications of the existing formalism, but geometrical applications remained paramount. I believe that physics is still too heavily reliant on the geometrical model of the vector - the displacement vector. Indeed, I have not found that the distinctive vector properties of important physical quantities such as force or angular momentum have been carefully worked out anywhere in the literature of physics.
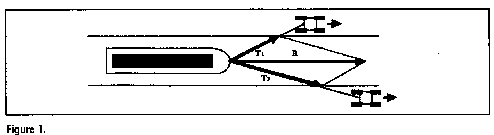
I find it helpful to begin vector graphics in terms of a series of concrete examples: abstraction and generalization can follow later. The displacement vector is easiest to explain, perhaps too easy. It is very different from other vectors such as force. Displacements are applied successively, they occupy different intervals of time, they involve a displacement through space and they are directly descriptive. Forces, on the other hand, can be applied at the same time and at the same point in space. Furthermore, the line representing a force is a geometrical analogue of the actual force and is not directly descriptive. These are important differences and there are many others. I have chosen to concentrate on the force vector here because of its importance. I choose tension in a wire or cord as the standard example of a force because it can be regarded as acting at a point. Other forces, such as surface friction and weight, are forces distributed over a surface or over a body, respectively. Suppose the force to be represented is a tension of 20 N applied by a marquee cord to a peg. The force can be represented geometrically by an arrow drawn to a suitable scale, pointing in the correct direction and applied to a definite point. I believe it is important to emphasize that the point of application of the force vector on your diagram represents a physical body. I also introduce the concept of the resultant, and the parallelogram of forces, in terms of an example such as tractors on opposite banks of a canal towing a barge. Our students will know intuitively that the combined effect of the tensions in the hauling ropes will be directed along the line of motion of the barge. It is also helpful to emphasize that both vectors represented in the graphical parallelogram are applied to the same body and at the same time. I have found that the most important point to make is that the resultant of two given forces is an imaginary force which is equivalent to the actual forces in the sense that acting alone it would have the same effect as the real forces combined. If we do not say this some may think that there are three real forces acting. We need to tell them that they must make a choice: either they deal with the original pair and ignore the resultant or they deal with the resultant and ignore the others. It is illegitimate to do both. This point can be emphasized by representing the resultant by a light line and the original forces by heavy lines (figure 1).
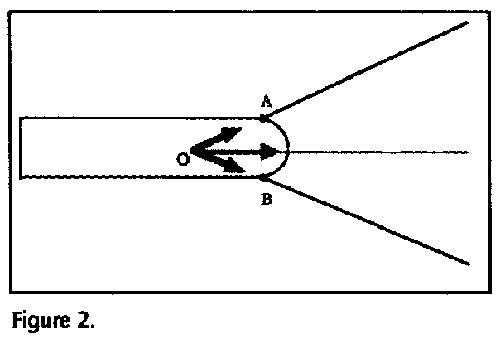
It is challenging to ask the class why the parallelogram algorithm works for forces. The line of action of a force can be introduced as an imaginary line of indefinite length coinciding with the force. On a rigid body a force can be applied with equal effect at any point along its line of action. The concept of the line of action is useful in simplifying representations (figure 2) and it is particularly helpful when calculating moments.
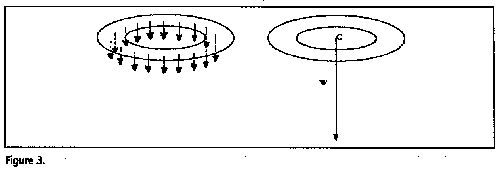
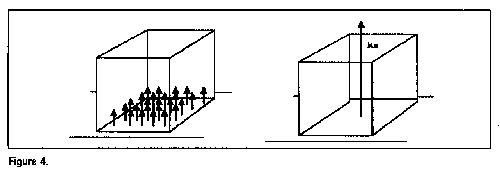
A common complaint about physics is that we do not explain why we are introducing certain concepts: we simply introduce them mathematically, without any justification. We may introduce the resultant as a tool of graphical calculation in an engineering drawing to find the combined effect of a set of forces, for example, or to simplify a problem. The most important example of the latter is weight thought of as a single force acting through the centre of gravity. The resultant weight is more convenient, both in explanation and in calculation, than the real weight, which is a force distributed over the whole body. This difference is brought out dramatically, for example, by the weight of a horizontal ring (figure 3). Another example is the reaction of a plane on the body it supports: in reality this is a force distributed over the undersurface of that body. We commonly replace it in thought, however, and on our diagrams, by its resultant represented as a single force acting on a point of the surface (figure 4).
The components of a single force are quite a different matter. A force such as weight, although it has a definite direction, is able to act in every other direction except a perpendicular direction: weight is able to roll a sphere along a plane with any inclination except the horizontal. The effective force in a given direction is called its component in that direction. It is calculated by multiplying the full force by the cosine of the angle made with the relevant direction. To avoid confusing our weaker students I believe it is important to introduce only one mathematical rule here and to calculate all components using the cosine rule. Any pair of perpendicular components is equivalent to the full force since, in combination, they have the same effect as the latter. In some cases a given force seems to divide naturally into such a pair. For example, the perpendicular (or normal) reaction and friction (the shear reaction) seem to be a more natural description of the action of an inclined plane on the undersurface of a sliding body than the total reaction. Components are sometimes introduced, therefore, to explain a physical process and not simply for mathematical convenience. Artificial vectors The position of the Moon with respect to the Earth may be specified by giving distance and orientation only. However, the position vector of the Moon provides distance, orientation and sense. The sense is chosen by convention to point from the Earth to the Moon. This artifice allows the position of a body to be treated as a vector and incorporated into the vector calculus. Area treated as a vector also has a directional sense by convention, only. The most subtle of all the artificial vectors are the axial vectors. Take the vector representing torque. This vector points along the axis of the torque. Our students know perfectly well intuitively that the action of a torque is in the plane of the torque and that, although it takes place around the axis, nothing actually points along the axis itself. If we tell them without qualification that the torque points along the axis, as is often done, we perplex them. I believe we should emphasize that axial vectors, such as angular velocity, torque and angular momentum, represent something going on around an axis and not along the axis. Processes of this sort, strictly speaking, cannot be represented by vectors since they do not point in just one direction. However, provided the students are willing to agree on a pure convention, they can be represented by a made-up vector. Notice that there are only two senses of rotation around a given axis, and only two arrow directions along that axis. This allows us to set up a one-to-one correspondence: we can agree by convention that an up arrow means a counterclockwise rotation - that of a right-handed screw - and a down arrow means the opposite. To represent a torque fully by graphics we then construct an arrow whose length represents the magnitude of the torque and whose arrow direction is linked by our convention to the sense of rotation of the torque. To verbalize this has taken me more than 30 years of frustrated
groping. I am confident it can be further simplified. It is interesting to note that both the axial vector and
the area vector are perpendicular to a plane and both have direction by convention only. Scalar algebra is still widely used, of course. I advise students to use scalar algebra to represent vectors where this is most convenient: the mathematics of physics is highly flexible and they should learn to use that form of mathematics which best suits the problem in hand. I emphasize, however, that vector algebra is often more economical and intuitive and is more convenient where the geometrical imagination is in trouble: in three-dimensional physics such as occurs in wave propagation, rotational dynamics and electromagnetism.. Vector algebra is often built upon sketch graphics but it is more abstract since graphics provide an analogue representation while algebra only provides a symbolic representation. If we return to the example of the barge, we can invite the class to symbolize the relationship between the two real forces and the resultant. Suppose they call the tensions T1 and T2 and the resultant R. Bold is used in print to emphasize that symbols represent directed quantities. We can verbalize the relationship as 'T1 combined with T2 is equivalent to R'. I then tell them that 'combined with' is commonly abbreviated by + in vector algebra ('bold plus' in printed notation) and 'equivalent to' is abbreviated to = ('bold equals'). So, the relationship becomes T1+ T2 = R. Do bold plus and bold equals here have the same meaning as the plain plus and plain equals of ordinary algebra? No. Meaning, as ever, is determined by context. I encourage the students to read + and = in their minds here as 'combined with' and 'equivalent to', respectively, until the idea sinks in. This helps them to avoid the usual ambiguities. I find with other teachers that the subtraction of vectors is best explained as the combination of a vector with a reversed vector. For example, v1- v2 = vr can be read as 'the actual velocity of the ferry ahead, when combined with the reversed velocity of our hovercraft, gives the relative velocity of the ferry'. We can interpret T1+ T2 = R, or any similar expression, as a statement of the quantity calculus symbolizing the relationship between the physical quantities themselves, and then it represents something concrete. We may equally well interpret it as an abstract statement relating graphical analogues or directed numerical values. All three interpretations are valid and we commonly shift from one to another. I find it difficult to introduce the scalar product and the vector product clearly. There is a tendency in some texts, which I can sympathize with, to introduce them abstractly as algorithms and then, much later, perhaps, to find physical examples to which they apply. In class this is unnecessary and I find it unhelpful. I may use the example of a body sliding a certain distance down an inclined plane. The work done by gravity is measured by multiplying the displacement d by the component of the weight along the plane, W cos(d^W), where d^W represents the angle between d and the weight W. Notice that the measure of the work, dW cos d^W, is the product of the magnitudes of two vector quantities and the cosine of the angle between them. This kind product turns up so frequently in physics that
it is given a special name and a special notation. It is defined as the scalar product of two vectors. It is scalar
because no direction is assigned or required in the outcome. It is symbolized by d
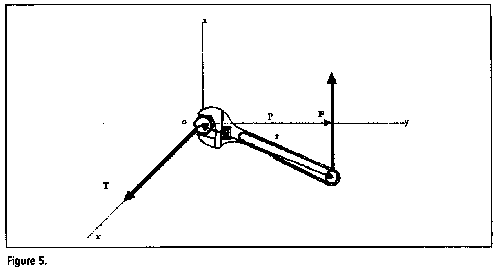
Torque and the vector product. yoz is the plane of action of the torque and ox its axis. The magnitude of the torque is given by the moment of the force F, which is equal to pF = rF sin rˆF. The conventional direction of the torque T is ox. This is symbolized by r X F = T in vector notation.
The vector product r X F (= T) is then defined as a vector of magnitude rF sin r^F and direction given by the following rule: curl the fingers of the right hand in the direction of rotation
of the torque. The thumb will point in the direction of the vector product. This needs to be tightened up, of course,
and generalized.
For mathematical purposes, I then argue, i cannot simply be placed beside 10: it must be interpreted as multiplied by 10 and so we have to turn
it into a mathematical object and give it a magnitude. The most convenient magnitude is the abstract and dimensionless
number 1, since multiplying 10 newton by such a number changes neither the magnitude nor the dimensions of the
force. Because i has this magnitude it is called a unit vector. The unit vector,
therefore, is an artificial vector which provides directional information only. We can put it anywhere in the diagram
- it is a free vector - and attach it to any physical quantity: it always gives the same information. j represents the unit vector in the y-direction and k that in the z-direction.
The weight of the teacher standing anywhere on the floor can be represented, for example, by W = -850k newton and the reaction of the floor on the teacher by R = 850k newton. From these beginnings we can build up the addition and
subtraction of vectors represented by their components. We can also use our definition of the general scalar product
and the vector product to prove that
Conclusions When we first introduce vectors I believe we should try to spell out what they mean. With this background our students can go on to manipulate them more confidently. I have attempted to give verbal expression here to what every experienced teacher already knows intuitively, if not consciously, about vectors. Although educated intuition in physics is not infallible or easily accessible it is immensely rich and should be treated with the greatest respect: it has, after all, built up over several millennia. Indeed, it is very optimistic to claim that one has faithfully articulated some elements of it. If one's efforts provoke controversy then one should think again. I would even go so far as to say, and I intend all of this to be self-referring, that the usual mathematical way of presenting vectors - which relies on a subsequent build-up of intuitive understanding - may be safer than an introduction using poorly thought-out explanations. Nevertheless, the attempt to articulate the tacit meaning of the concepts of physics is highly important, and not only for teaching. If parts of the meaning of many of the concepts of physics are grasped intuitively, only, can physics be said to have full rational control over its concepts?
Further reading
|