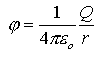|
Applying the history of electricity in the classroom: From Teaching the History of Science ed Michael Shortland and Andrew Warwick (Oxford: Blackwell, 1989), 168-184 (slightly modified)
John Roche Linacre College, Oxford, OX1 3JA Email: john.roche@linacre.ox.ac.uk Reviving the Arts of ExplanationThere appears to be a growing interest among scientists and science teachers today in the historical dimensions of their subject. There have always been teachers, of course, who have recognized that a knowledge of the historical evolution of any topic gives a deeper understanding of it than that which is provided by textbook knowledge alone. What we are now witnessing, perhaps, is the beginnings of a general movement to integrate past and present in science as a means of consolidating and clarifying foundations. My chief concern in this essay is to show that historical research by teachers can be a powerful tool in physics teaching, especially in the clarification, explanation, and exploration of physics concepts. [1] I shall take the concept of electric potential as a case history exemplifying this method. Before I can begin it is necessary to defend this approach from an opinion current among some physics teachers and lecturers. According to this view false or made-up history can be an acceptable aid in teaching physics, much as Aesop’s fables may be used to teach certain moral lessons. Aesop’s fables, however, are indeed called fables, whereas the fabulous history of physics is usually presented to students as true. Historical fables in physics must surely falsify and deform scientific thought and method, since it misrepresents them. Accurate history of physics, on the other hand, lays bare the roots of modern concepts and illustrates the scientific mind as it really works. This chapter is chiefly concerned with a particular historical development in physics which must strike anyone who compares Faraday’s writings on physics with those of any modern physics textbook. Physics has become progressively more mathematical in the course of the past two centuries. As a result the arts of verbal explanation are now neglected in physics, or, at least, have not been developed to the same extent as mathematical and experimental presentations. School teachers, teacher training colleges, and educational institutes have, of course, a strong professional commitment to clear verbal explanation. But the efforts of even the most brilliant teachers and lecturers are often hampered by the poor quality in physics today of the available techniques of qualitative definition, classification, description, drawing distinctions, and applying explanatory terms. These skills still thrive outside physics, of course, in biology, law, engineering, and in popular science, for example, but physics is particularly difficult to explain rigorously and clearly, and it requires the development of a broad and sophisticated resource of special explanatory concepts which can match adequately the complexity of the subject. I believe that such concepts can be developed, not simply by abstract reasoning, but also in the context of the effort to explain physics clearly in class. I also believe that this effort is assisted by a knowledge of the history of physics. I shall now develop each of these notions in more detail. Every class in physics can be a fertile experiment in explanation. Physics teachers in the classroom learn to key their explanations to the explanatory expectations of the students. The students are already familiar with informal methods and categories of explanation drawn from everyday life and from many other disciplines. This is an extraordinarily rich resource which the physics teacher can draw upon and refine. It also has the enormous advantage that the student understands it and will understand physics explanations expressed in its terms. It is common knowledge among physics teachers and educationalists that there are topics in physics which most students find difficult to understand. These include mechanics, electrostatics, electromagnetic induction, and thermodynamics. It is often assumed that the physics teacher who is bright enough and who labours sufficiently at preparation, presentation, and correction will be able to explain these difficult subjects clearly. This, I believe, is not always true. There are many topics, even in school physics, which no-one in the profession yet understands clearly. It is not that there is any missing evidence. It is because of the underdevelopment of verbal explanation, as I have suggested. Physics, I believe, has not yet recognized the importance of creating an adequate repertoire of carefully selected and uncontroversial explanatory concepts and terms which can be used to explain difficult topics clearly. There is, of course, a considerable body of successful explanatory concepts already available in physics, but this needs to be improved upon and greatly extended. Reformation of this sort, rather than some new revolution is, I believe, needed in physics to-day. To my knowledge there are no research institutes, staffed by physicists, which are devoted exclusively to clarifying, explaining, and understanding the foundations of established physics. All able physicists are busy pushing back the increasingly remote frontiers of science. Understanding physics seems to be low-priority knowledge which one picks up casually while studying, teaching, supervising laboratory work or carrying out one’s own research. Nevertheless, most would admit that clear understanding is the key to progress in physics, and the lack of understanding is the cause of much intellectual distress and alienation from physics. Furthermore, understanding a difficult concept is one of the most satisfying intellectual experiences known to man. History, I believe, is essential to any endeavour to improve the quality of understanding and explanation in physics. Many, if not most, of the difficult topics in physics teaching can be made understandable only by joining a thorough familiarity with the modern theory to research into their historical origins. There seem to be two main reasons for this. Firstly, history lays bare the roots of the modern theory and this often reveals that misinterpretations, errors, and obscurities have worked their way into the very foundations of the theory and have never been cleared up subsequently. Secondly, a difficult topic, seen through the prism of history, often turns out to be a nexus of competing traditions and conceals a variety of distinct problems. In other words, concepts which should be carefully distinguished sometimes posture as a single concept. When all of this is understood in detail many difficulties become much easier to resolve. The Prism of HistoryAfter these general remarks some concrete examples will help to make my meaning plain. One kind of difficulty inherited from history is obsolete technical language. This is only a problem, of course, when the individual teacher, or the physics profession as a whole, fails to recognize a certain term as redundant. The ‘permittivity of a vacuum’, implying as it does an electrical property of the vacuum or free space, was introduced late last century by Oliver Heaviside (1850-1925), [2] because it was widely believed that space is filled with a material aether which permits the passage of the electric field to a definite degree. [3] Today, the physical constant so named is known to be the ‘electric interaction constant’ [4] between charges, analogous to the ‘gravitational interaction constant’ between masses The term permittivity of a vacuum is, therefore, obsolete Nevertheless, it lingers on. Other examples of obsolete terms are electromotive force, which is usually used to mean a voltage rather than a force, ‘magnetic coercive force’, which is a magnetic field strength, and the ‘permeability of free space’. Another closely related source of explanatory difficulties may be due to a lack of awareness that there are remnants of falsified theories which still survive in various odd corners of modern textbooks and research literature. Since the last century there have been at least nine competing theories of the electromagnetic field. [5] Only one of those is generally accepted to-day, but remnants of the others, often unrecognized for what they are, still struggle to survive on the margins of modern electromagnetism. I am not criticizing their right to survive, but I am criticizing mixed or incoherent explanations which result from a lack of historical knowledge of the evolution of electromagnetism. Falsified theories may still be useful, of course, as conventional or fictional explanations. For example, the use of magnetic poles is an easier way to ‘explain’ many magnetic phenomena than the true force between electric currents. Such ‘explanations’ may still be used harmlessly, provided their fictional or conventional character is made quite explicit. In many cases, however, this is not brought out. A good example of this is the so-called catapult field in electromagnetism. It is not difficult to imagine the perplexity generated by teaching in one class, correctly, that the applied magnetic field exerts a force directly on the moving electrons in the wire, and in the next class teaching, incorrectly, that the force on the conductor is due to an interaction between the applied magnetic field and that due to the moving electrons in the wire. In modern macroscopic electromagnetism there is no interaction between magnetic fields themselves, and no tension in the lines of force. Fields act only on charges, not on each other. To consider another example, it is not yet clearly understood in physics, I believe, that the force between two bar magnets is not composed of forces between the poles. In fact, each part of a magnet contributes a roughly equal amount to the total force. This total force can indeed be notionally resolved into components which act between the poles, but the true force is a distributed force. Following Faraday it is often said that an iron sphere ‘shields’ its interior from an external magnetic field. This, according to strict modern theory, is incorrect. The applied magnetic field passes right through the iron undiminished. It then induces a secondary magnetic field in the iron. The resultant of these two fields gives rise to a balanced field in the interior. It is best, perhaps, to call this process ‘effective’ shielding. No teacher or lecturer or textbook writer deserves criticism for making any of these mistakes — they are quite endemic and are usually unrecognized within the profession. Historical research lays bare the origins of these difficulties and goes a long way towards clearing them up. Problems of this sort cannot be resolved by long hours of pondering over modern texts. This can be amateurish and misleading because it is most likely that the very concepts which need to be cleared up have long been internalized and, without critical history, will infect and obscure the effort to analyse them. He who is not part of the historical analysis is almost inevitably confined to the received synthesis. Origins of the Concept of PotentialAs a case history illustrating the method of research which I call ‘critical physics’, I shall consider the difficult concept of electric potential or voltage. The physics teacher or lecturer is prompted to mull over this concept year after year in the course of class preparation and delivery. If he or she is also provided with a knowledge of the evolution of the concept then there is an enviable opportunity to treat each class on the topic as a workshop in which new or modified explanations of potential can be proposed and tested against the common sense understanding of the students. This should lead to a much improved explanation of potential, one which gathers together all of the valid insights of the past, goes beyond them where necessary and fashions a more comprehensive, unified, and coherent concept. In the context of the classroom itself, therefore, the schoolteacher or tutor has the opportunity to carry out important foundational research in the concepts of physics. How can historical research prepare the ground for such an improved concept of electric potential? A sketch of the evolution of the concept should help to make this clear. The modern concept of potential is the fusion of at least five quite distinct historical traditions. Despite the seeming unity of the received concept, each of these traditions still plays a semi-autonomous role in the present-day understanding of potential. One of the earliest hypotheses concerning the nature of potential was that of William Watson (1719—1787), who proposed the view in the late 1740s that the electric fluid is in a state of compression or pressure. Henry Cavendish (1731—1810) developed this view further in the 1780s. [6] The concept of potential as a pressure can still be found in textbooks and other literature today, sometimes as an analogy and at other times as a literal explanation. Although this explanatory tradition is now marginal it illustrates how a tradition of explanation, once launched, seems to remain in service for ever. In a publication of 1779 Allcsandro Volta (1745—1827) introduced his powerful concept of ‘the degree of electric tension’ of a charged conductor.[7] He showed how this ‘tension’ could be measured and he transformed it into a successful working concept. It was immensely influential. It even gave rise to Faraday’s concept of tension along the lines of force, and influenced Maxwell’s theory of stresses in the aether. Volta’s concept of tension survives in electrical engineering where expressions such as ‘high-tension lines’ are still used. Volta also introduced the concept of ‘electromotive force’ as the prime mover of a current in a closed circuit, and measured it in terms of his electric tension.” G.S. Ohm (1789—1854) in 1827 attributed the concept of ‘electroscopic force’, or tension, to circuit resistors, a concept now known as the voltage across the resistor. [9] It should be noted that these early concepts drew heavily on mechanical analogies. Furthermore, although electric ‘pressure’ or ‘tension’ was thought of as a property of the electric fluid in a conductor, it was not thought of as a property exercised across the neighbouring space. This extension of the concept was added later in the nineteenth century. A very different concept, that of electric ‘potential’, was introduced in the early nineteenth century not by experimentalists, such as Watson and Volta, but by the mathematical physicists Poisson and Green. S.D. Poisson (1781—1840), in 1811, strongly inspired by Laplace, introduced a mathematical function to electrostatics whose gradient was numerically equal to the local electric intensity, or force per unit charge.” This was a very convenient function because it was non-directional and easier to handle mathematically than the electric intensity function. It is important to note that the potential function was introduced to electrostatics as a mathematical artefact only, and not as a physical state. George Green (1793—1841) of Nottingham, in 1828, invented the term ‘potential’ for the potential function and developed its mathematical properties much further. The potential function had a fixed value on the surface and in the interior of an electrostatically charged conductor, but it also had values in space everywhere in the neighbourhood of that conductor. J.L. Lagrange (1736—1813) and C.F. Gauss (1777—1855) introduced and developed the mutual potential energy function, which is related to the potential function. This function was also thought of at first as a mathematical construct only. [12] The next major step in the evolution of the concept of potential was made by Gustav Kirchhoff (1824—87), who effected a synthesis in 1849 which showed that Volta’s tension and Poisson’s potential function were numerically identical in a conductor and that they should, therefore, be reduced to a single concept. He also associated the new concept with electrical energy. The concept of potential does not seem to have developed very far beyond the point at which Kirchhoff left it in the middle of the nineteenth century. There is now a cluster of at least four concepts which are closely related to each other and yet are thought of as somehow distinct, namely potential, e.m.f., circuit voltage, and electrical potential energy. Engineers and teachers are quite confident that voltage is a genuine (and dangerous) physical property, while some theoretical physicists still suppose with Poisson and Green that potential is a mathematical artefact only. All of this suggests that a considerable effort is now required to distinguish, clarify, and formulate a coherent theory of potential. Suggestions for the Clarification of the Concept of Potential Introduction The argument which follows attempts to be systematic, since it might be tedious for the reader were I to try to describe the steps by which I arrived at this interpretation of potential. Suffice it to say that I have applied the methods outlined earlier in this article, namely historical study, the analysis of concepts, and trials in class. Although this effort has gone on for almost thirty years I feel that there is still much to be done. Indeed, I believe that the work of clarifying and understanding the concept of potential, and of all other concepts in physics, will never end. Potential energy There appear to be at least two kinds of electrical potential energy, namely mutual potential energy and individual potential energy. The mutual potential energy of a system of charges may be defined as the total energy available in that system to supply to the charges composing it, while these are being withdrawn to a great distance from each other. It may be positive or expulsive, or it may be negative or binding. The mutual potential energy of a system of charges is zero when all charges are electrically remote from each other. A more frequently encountered type of potential energy in physics is the potential energy of a single charge with respect to a fixed system of charges. The individual potential energy of that charge is the work which the system of charges will do on it, while it is being fully withdrawn from the system, the other charges remaining fixed. The energy given to a proton released near the surface of a positively charged Van Dc Graaf generator, and driven far away, is a positive example of individual potential energy. The ionization or escape energy required by an atomic electron is an example of negative individual potential energy. Individual potential energy is usually called absolute potential energy in order to distinguish it from relative potential energy. The latter concept is familiar in elementary gravitational theory where the relative gravitational potential energy of a given body with respect to an arbitrary reference level is the work which the system is ready to do on the body as it is transferred from its starting point to the reference level. Relative electrical potential energy is similarly defined. It is used, for example, in discussions of excitation and dc-excitation of electrons in atoms. The absolute potential energy of a given charge at rest with respect to a system of charges (also at rest) is a true physical state, since a system loses rest mass when a charge with expulsive potential energy is removed, and gains rest mass when a bound charge is withdrawn. A charge has zero absolute potential energy with respect to a given system of static charges when it is far away from that system. This follows from the consideration that no work will be done by the source charge on the test charge as it is further withdrawn, and absolute potential energy is defined precisely in terms of the latter process. Although it has no absolute potential energy a remote charge has an infinity of relative potential energies with respect to points in the neighbourhood of the source charge. Electric potential of static charge distributions Electric potential is explained and defined in terms of individual rather than mutual potential energy. When a test charge is withdrawn far from a system of fixed charges the work done per unit positive charge is independent of the magnitude of the charge.
By analogy with the expression ‘intensity of electric force’, which is the general meaning of ‘force per unit charge’, I shall describe the electric potential in general, at a given point, as ‘the intensity of the potential energy of charges placed there’. When we think of potential at a point, therefore, in this interpretation, we must suppose some charge there in possession of that property. If no such charge is present then potential is a virtual rather than an actual property at that point. Together with an explanatory definition of potential a measuring definition is, of course, required in order to make the concept physically complete. The present standard measuring definition of potential at a point is the work done by an agent against electrical forces, per unit positive charge, in transferring a test charge from infinity to the point in question. The term ‘infinity’ is introduced here for mathematical convenience only, since, in an actual measurement, it is sufficient for the starting point to be far enough away from the source of the potential so that the electrical effects of the source are negligible. If the measuring convention were specified in terms of the electrical work done by the source system itself, per unit positive charge, on a test charge which exits from the system, this would be in better agreement with the physical concept of potential as I have explained it above. There are several other advantages as well. As a working concept in physics, potential is used where the electric forces themselves do the work, not some notional agent. The received definition, therefore, displaces attention from the physics of the situation. Next, the new definition leads to a more natural algorithm for the potential function. Finally, the new conception, unlike the old, is not likely to be confused with the concept of relative potential energy discussed above. Both conventions, of course, give the same magnitude and the same sign to the potential. Whatever the exit path chosen for a test charge from a given point in the neighbourhood of a system of stationary charges, the intensity of the electrical work done on it will be the same. Furthermore, the total electrical work done in any closed path is zero. Systems of force with this property are called conservative. Since possible exit paths radiate from a given point in all directions, and since the terminal point chosen is arbitrary, absolute potential has no specifiable direction. It is, of course, unique and single-valued and zero at points electrically remote from all charges. Furthermore, it is positive or negative depending on the sign of the source charge. The absolute potential at any point which is electrically remote from a given system of charges is zero with respect to that system, since the absolute potential energy of charges placed there is zero. The absolute potential at a point which is electrically remote from all charges will, of course, be absolutely zero. Those who suppose that the absolute potential at a point in empty space can be given arbitrary values are clearly treating it as a mathematical artefact only, and are carrying to an extreme the purely mathematical interpretation of Laplace, Poisson, and Green discussed above. However, when interpreted as the intensity of exit energy, absolute potential has a well-defined physical meaning which is analogous to the specific latent heat of sublimation, for example. Auxiliary non-physical potential functions can, of course, be very useful, but only the absolute potential deserves to be included in the physically descriptive equations of electromagnetism. In order to distinguish auxiliary from physical potential functions, it is helpful to think of the latter in relation to the charge system which causes it, and not abstractly. Mathematically speaking, the expression
associates a definite numerical value of the potential function Some properties of the electric potential The potential difference between two points is the difference in absolute potential between them. This property is inadequately defined unless the starting point A and the terminal point B are specified. The potential difference is then the final value less the initial value, Absolute potential decreases most rapidly in the direction of the field. Respecting direction, it is easy to show that the electric intensity is equal to the negative potential gradient, Adding a positive charge anywhere in space increases the absolute potential everywhere in its neighbourhood, because its presence creates an additional commitment to supply energy to every exit path radiating from every neighbouring point. The addition of a negative charge, or the removal of a positive charge, similarly reduces the neighbouring potential everywhere. An uncharged insulator placed in the neighbourhood of a positive charge acquires the potential previously possessed by that region of space which it now occupies. A charged conductor which is placed in the vicinity of another charge will have a resultant potential which is partly due to its own charge and partly due to the neighbouring charge. The interior of the conductor will also have a potential since any path from its interior to any electrically remote point will be an electrical energy supply route. When a conductor of higher potential is joined to a conductor of lower potential, positive (conventional) charge must flow from the former to the latter because a mean negative potential gradient implies an average positive electric field, which will drive the conduction charges in the connecting wire. Any charges on the Earth’s surface or in the atmosphere locally, will contribute to the absolute potential of a given conductor or insulator. Instead of dealing with the absolute potential of a conductor it is often more convenient to deal with its potential relative to the local Earth’s surface. Each plate of a charged capacitor will have an absolute potential which is partly due to its own charge, and partly due to the charge on the opposite plate. The potential difference between the plates is simply the difference in these absolute potentials. When an uncharged dielectric is inserted between the plates of an isolated capacitor the charges
on the plates cause a displacement of positive electricity in each atom towards the negative plate. This increases
the absolute potential of the negative plate. Similarly negative atomic charge is displaced towards the positive
plate, reducing its It should be clear from all of this that absolute potential can only be understood clearly when it is closely linked in thought to the charge which causes it. Voltage Electric potential is produced only by charge systems which are not electrically neutral. However, electrically neutral bodies can produce forces which do work on charges - even in the absence of absolute potentials or potential differences. When a magnet is moved along the axis of a closed circular conductor, for example, the induced electric field of the magnet drives a current around the circle without the presence anywhere of potentials, potential differences, or unbalanced charges. There is a need, therefore, especially in circuit theory, for a broader concept of the intensity of electrical work which is able to encompass all cases in which work is done on charges. In circuit theory also, it is necessary to be able to specify the sense or direction in which work is being done. The concept of voltage satisfies both of these requirements. The magnitude of the voltage between two points is the work done per unit positive charge passing between the points. The sense of the voltage is that of the field or conventional current passing between the points. Voltage, like magnetic flux, is an example of a quantity with sense but not direction. Voltage is not a vector. Voltage is always specified between two points or bodies or around a circuit. There is no absolute voltage at a point. In a resistor carrying a current, for example, the sense of the voltage is that of the conventional current, or of the driving electric field, since that is the sense in which positive work is being done on the conventional current. In a charged capacitor the sense of the voltage is from the positive to the negative plate, through the capacitor itself The sense of an e.m.f. is the sense in which it freely drives the conventional current through itself When a charge of arbitrary sign passes in any direction between two points which have a voltage V between them, the work done by electrical forces on the charge is given by W = ± QV. The discussion above makes clear which sign should be chosen. Electromotive force Electromotive force has two meanings in physics. It means the prime mover of the electric current in a circuit, and it also means the voltage across that prime mover. I shall reserve the abbreviation ‘e.m.f.’ for the latter meaning only. The most important cases of electromotive forces for the present study are those operating in voltaic cells and in electromagnetic induction. In a cell the prime mover of the current in the circuit is a very short-range electrochemical force-field which is localized in the contact zones between electrode and electrolyte. Induced currents are primarily driven by more extensive induced electric fields, or by magnetic fields, which are, nevertheless, usually confined to only a small portion of the circuit. Electromotive forces are non-conservative. This means that they can supply energy to charges which move in a closed circuit, unlike electrostatic force fields. Electromotive forces, although they may be localized in a small part of a circuit only, nevertheless drive a uniform current throughout the circuit. This happens as follows. The charges which are driven out of the active zone, in the first instance, become excess charges and drive onwards those conduction charges which are ahead of them. A corresponding process of attraction occurs at the negative end of the active zone, and in succession all around the circuit, causing a current to flow everywhere. At each point of the circuit the excess charges there repel each other and travel immediately to the surface of the conductor. As a result a surface charge gradient is established all around the inactive zone, ranging from positive at the positive terminal of the e.m.f. to negative at the negative terminal. These surface charges set up an electric field which is the driving agency of the current in this part of the circuit. The auxiliary charge distribution itself is maintained and energised by the e.m.f. In the zone occupied by the e.m.f. there will, of course, be a reversal of charge gradient, which is gradual for an induced e.m.f., but quite sudden in the contact region between the poles and electrolyte of a cell. This means that there will be a reversed electric field in these zones which is in opposition to the local e.m.f., and which ensures, among other things, that the current there is no greater than that in the rest of the circuit. Since the fields produced by the auxiliary surface charges are conservative, it follows that the voltage across these fields outside the region of the circuit containing the e.m.f. must be exactly equal and opposite to the voltage across the corresponding conservative or coulomb fields within the region occupied by the e.m.f. If the sense of the e.m.f. is chosen as the positive sense of circulation, then the net internal voltage will be the difference between the e.m.f. and the coulomb voltage. It follows, therefore, that the algebraic sum of the net internal voltage and the external circuit voltage will be exactly equal to the e.m.f. This means that all of the energy supplied to a charge as it passes once around the circuit comes ultimately from the e.m.f. In a voltaic cell the net voltage between the poles measured internally is simply the voltage across the electrolyte resistance, since the coulomb voltage virtually balances the e.m.f.’s in the contact zones. On open circuit, this net internal voltage is zero and the external coulomb voltage is exactly equal in magnitude and circulatory sense to the voltage across the internal electromotive force. When the circuit is closed, there is a fall in external voltage which is exactly balanced by a rise in the voltage across the electrolyte. In a transformer or inductor winding, the net internal voltage is again the voltage across the internal resistance only. If a unit charge is taken once around a circuit the total work done on it by the resultant fields is the sum of the net voltages in each circuit element, which may include cells, capacitors, resistors, coils, and even air-gaps. But the work done on the charge in this closed circuit by the purely conservative fields present must be zero. These therefore drop out of the sum and only the non-conservative e.m.f.s remain. Hence Kirchhoff’s second network law follows: that the sum of the underlying e.m.f.s in any closed circuit is exactly equal to the sum of the net voltages in exactly the same circuit. Absolute potentials in a current-bearing circuit In describing electric circuits it is clearly important to distinguish carefully between two interacting structures, namely, the auxiliary surface charge system which is conservative and which creates an absolute potential at every point of the circuit, and the electromotive forces which are not conservative and which do not contribute to the absolute potentials. It is also necessary to distinguish between the absolute potentials and voltages in a circuit. The absolute potential of any point of a circuit is essentially an external property of the circuit, since it relates to exit energy. Furthermore, it is almost always a latent or inactive property. Voltages, on the other hand, are internal properties of circuit elements and measure active energy processes. This means that when internal processes only in a circuit are being discussed, there may be no need to introduce absolute potentials or even potential differences. For example, only e.m.f.’s and voltages appear in the above statement of KirchhofFs law. When separate circuits, or separate branches of a single circuit are being compared, however, it may be necessary to introduce potentials. For example, the action of a potentiometer can be explained by stating that the galvanometer current is zero because the absolute potential of the slider is the same as that of the point of the potentiometer wire where it makes contact. It is also important to note that a current-bearing circuit can be electrostatically charged, just as any conductor can be charged, but there are peculiarities. Since the absolute potential varies from point to point around a circuit, the amount of charge which flows into the circuit from a given charged conductor will depend on the potential of the point of contact chosen and on the potential of the charged conductor. If, for example, any point of a circuit is joined to the Earth, charges will flow to reduce the potential of that point to earth potential. These charges will spread over the whole circuit and the inflow (or outflow) will cease only when the absolute potential of every point of the circuit has been reduced by an equal amount. Of course, only one point of the circuit will be at earth potential, and only the absolute potentials and the surface charges and fields are affected by earthing, not the circuit voltages, nor the differences in absolute potentials. Earthing a circuit protects the absolute potentials of a circuit from random fluctuations caused by local movements of charge and by accidental contacts. Sign conventions and terminology When Kirchhoff’s second network law is applied to a circuit, two sets of sign conventions must be introduced in sequence to each of the circuit elements. In the first stage the e.m.f.s and voltages are given their proper directions, if known, or, if not, are assigned tentative directions. In the second stage a clockwise or counterclockwise circulation convention is chosen, for convenience, for each sub-network. An additional positive or negative sign is then attached to each e.m.f. or voltage symbol, depending upon its direction in relation to the circulation convention. As in geometrical optics, these conventions, if applied consistently, allow a single general formula to be applied correctly to all cases. For example, when a cell is applied to a resistor, the voltage across the pure electromotive force of the cell, that is, the ‘e.m.f.’ of the cell, is in the same sense as the voltage across the resistor, when measured with respect to the circulation convention in the circuit. Not only does the resistor voltage not ‘oppose’ the e.m.f., it is the agent of the latter in supplying energy to the current. When a capacitor discharges through a resistor, the voltage across the capacitor and that across the resistor are in opposite directions, again with respect to the circulation convention in the circuit. This is so because, in such a circuit, which contains no e.m.f., all fields are conservative and the net voltage around any closed circuit must be zero. It is sometimes stated that a capacitor charges up until its voltage ‘balances’ the e.m.f. Here, the capacitor voltage and the e.m.f. act in the same circulatory sense and they act through different bodies. It follows, therefore, that they cannot balance each other. However, the electrostatic voltage between the charges on the battery terminals measured through the battery does indeed balance the e.m.f., when the capacitor is fully charged. Conclusion I would recommend a sharpening of the conceptual, verbal, and notational distinctions which are
already made, although not very consistently, in this subject by physicists. I believe that it would clarify explanations
and practical usage were the term ‘potential’
and the symbol I would finally recommend that ‘electromotive force’, understood as the prime mover of electric current, be carefully distinguished from ‘electromotive voltage (e.m.v.)’, understood as the voltage across that prime mover.
1 Roche (1987). 2 Heaviside (1892).
4 Concise science dictionary (1984). 5 Whittaker (1961, 1962). 6 Watson (1747), Cavendish (1879), Heilbron (1979). 7 Volta (1779), p. 262. 8 Roche (1987). 9 Ohm (1841), p. 403. 10 Poisson (1811). 11 Green (1828). 12 Lagrange (1867-92), 4, pp. 402-3; Gauss (1841), p.176. 13 Kirchhoff (1883, 1850).
Cavendish H 1967 The Electrical Researches of Henry Cavendish ed J Clerk Maxwell (London: Cass, 1879, reprinted 1967). Concise science dictionary 1984 (Oxford: Oxford University Press) Gauss C F 1843 `General propositions relating to attractive and repulsive forces' in Scientific Memoirs ed R Taylor, 3 (London), 153-196. Green G 1828 An Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnetism (Nottingham). Heilbron J L 1979 Electricity in the 17th and 18th Centuries (Berkeley: U California Press). Kirchhoff G 1850 `On a deduction of Ohm's laws in connection with the theory of electrostatics' Phil Mag, 37, 463 468. Kirchhoff G (1882) Gesammelete Abhandlungen (Leipzig). Lagrange J L 1867-1892 Oeuvres (Paris) Ohm G S 1841 `The galvanic circuit investigated mathematically' in Scientific Memoirs ed R Taylor (1841-1852), 2, 411 5. Poisson S D 1811 `Mémoire sur la distribution de l'électricité à la surface des corps conducteurs' and `Second mémoire sur la distribution de l'électricité à la surface des corps conducteurs' Mem Cl Sci Math Phys Inst Imp France, 12, Année 1811, 1 92 and Année 1811 part II, 163 274. Roche JJ 1987 ‘Explaining electromagnetic induction; a critical re-examination’, Physics Education, 22 (1987), 91-99 Volta A 1779 `Observations sur la capacité des conducteurs électriques...' J Phys, 13 (Paris), 249 277. Copyright ©: John Roche 1989 and 2001
|
with every point r in the neighbourhood of the source charge Q. Physically speaking, however, this can be misleading. From a physical point
of view potential is a commitment of the system to supply energy along a stellation of exit paths from the given
point. It is not, therefore, a property localized at the latter point, such as the electric force on a charge placed there.
reserved for ‘absolute potential’ or the difference
between two absolute potentials, only. ‘Voltage’ and the symbol V seem best reserved for the concept, already established
in circuit theory, of the directed work done by local electrical forces, per unit charge, along paths between two
designated points. This means that we may correctly speak of the ‘voltage
across’ an electromotive force, or the ‘voltage
between’ capacitor plates, but it means that expressions such as ‘voltage difference’ or ‘voltage
drop’ become as meaningless as ‘work difference’ or ‘work drop’. It also implies,
for example, that the ‘voltage of a conductor’ and
the ‘potential drop across an e.m.f.’ are both
incoherent expressions.