|
[HomePage] |
Professor W.W. Sawyer | |
The Contribution of Music to Mathematical Discovery
WW Sawyer
Mathematicians, it is often said, tend to be musical. It is less well
known that problems arising from music have played an important role in the discovery of fundamental mathematical
ideas. Questions about the vibrations of a piano string led to a fierce controversy that forced mathematicians
to clarify their ideas about area, continuity, and the convergence of series.
It is well known that there exists a mathematical theory of musical sounds. Very few people know that music has
made a contribution to mathematics. In fact a suggestion made by a musician led to a total revolution in the way
mathematicians approach their subject. No doubt, mathenaticians would have made this step forward sooner or later
if the musician had not given this hint, but as a matter of historical record, that was how it happened.
Vibrating Strings
In the 17th century, calculus provided mathematicians with a splendid instrument for investigating gradients and
velocities, and mathematicians enthusiastically set about investigating anything that had a shape or that moved.
One of these topics was the vibrations of a piano string.
'
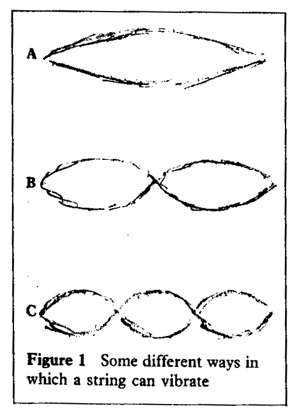Figure 1 shows some of the ways in which a string can vibrate: A produces a certain note; B produces the first harmonic, an octave higher; and C fifth higher.
In 1715, the English mathematician Brook Taylor gave this a mathematical form.
If we choose a suitable unit of time and a unit of length that makes the string have length 
, the displacement of the string at position x and time t is given by
y = sin
x cos t for vibration A
y = sin 2x cos 2t for vibration B
y = sin 3x cos 3t for vibration C
There are of course harmonics beyond these, corresponding to the numbers 4, 5, 6....
So far, these vibrations are separate possibilities. However the French composer,
Rameau, said that when a note was played he heard many of these harmonics at one and the same time. In 1726 he
published a theory of harmony (which I believe is still regarded as valid) based on this idea.
Mixtures of Harmonics
The Swiss mathematician, Daniel Bernouilli, picked up this hint. He formed an arbitrary mixture of all the harmonics
and thus in 1753 arrived at the formula
y = a1 sin x cos t +
a2 sin 2x cos 2t + a3 sin 3x cos 3t + .....
It is interesting that Bernouilli's argument is based purely on physics; there are no calculations in this part
of his paper. He speaks of 'a melange of all these vibrations' and goes on to say, 'All musicians are agreed
that a vibrating string gives at the same time, besides its fundamental tone, others much higher; they notice above
all the mixture of the 12th and the major 17th'.
His series contains an infinite number of constants an which can be chosen at will. Bernouilli expressed the
belief that this series represented all the vibrations possible when a stretched string was put in some position
and released from rest. The initial shape of the string is found by putting t = 0. Then all the cosines have the
value 1 and the series becomes
y =
a1 sin x + a2 sin 2x + a3 sin 3x +
... +ansin nx+ ... (1)
According to Bernouilli, every possible starting shape of the string could be shown by such a series.
Violent opposition to this view came from the French mathematician d'Alembert and the famous Swiss mathematician Euler. Indeed mathematicians argued for the next fifty years without getting any further forward. Euler and d'Alembert pointed out that the simplest way to set a string vibrating was to pluck its middle point and give it the shape in Figure 2.
This shape consists of two lines with different equations. They maintained that
it was impossible for the single formula (1) to start off representing one line and then halfway through, change
its mind and decide to represent another. If it started off representing part of one line, then it had to go on
for ever showing that line.
Fourier Series
This was in fact true for all the formulas they had met up to that time. If two polynomials have exactly the same
values when x lies in some interval
(however short) they must be equal for all x.
The same is true for combinations of functions such as sin x, cos x,
ex, in fact for almost
anything you might meet today in a sixth-form textbook. It is also true for power series, that is, series of the
type
c0 + c1x + c2x2 + ... + cnxn
+ ...
provided you take account of convergence. But the series (1), known as a Fourier series, is an entirely new type
of creature. The graph in Figure 2 actually corresponds to the series
with quite a simple rule for the coefficients. Yet it is able to represent parts of two different lines.
However there is worse yet to come. Usually, when we are drawing graphs, they turn out to be continuous, that is
to say, there are no breaks in them except perhaps when they go off to infinity as does y = 1/x near x =
0. This is no longer true when we are dealing with Fourier series. For instance, there is a Fourier series that
gives F(x) with the graph shown
in Figure 3.
This series converges in much the same way as the geometrical progression with
a common ratio of 1/2. Now f(x)
shows a break at every point at which one of the terms has a break - that is to say, at every place where 
is a fraction of which
the denominator is a power of 2. These points are so close together that it is impossible to draw the graph; there
are no two points joined by a continuous piece of curve. Yet there is a Fourier series for f(x).
This is a simplified account of an argument given by Bernhard Riemann in 1854 in a dissertation 'On the representability of a function by a trigonometric series'. With regard to functions like f(x) that cannot be drawn, he says, 'Such functions have never been considered before'.
Coefficients in the Fourier series can be calculated by integrating the function. Since f(x) has a Fourier series, we naturally consider whether it can be integrated. Riemann showed that it could. This remarkable result means that although the graph of f(x) cannot be drawn, there is a definite area under it.
It is also remarkable that one can combine the curves of sine graphs to produce straight lines, and that one can combine sine curves, which are continuous, in such a way as to produce the gap in Figure 3, let alone the infinity of jumps that are seen in the graph of f(x).
The Nature of the Change
It is typical of the facts that Fourier series reveal to us, that they are not what we would expect - at any rate
at first glance.
The Germans have a rather good term, 'Anschauliche Mathematik' - mathematics that you can understand by looking at it. The corresponding English word is 'intuitive' - mathematics that you feel should be true. In the 17th and 18th centuries, mathematics was essentially intuitive; mathematicins used procedures that looked right and seemed reasonable. It was in this spirit that calculus was discovered and it is still in this way that learners should be introduced to the beginnings of calculus. Indeed intuition is still important at the stage of advanced work; it is essential to have a feeling for what you are doing.
The 19th century was the century of rigour. The free and easy style of the earlier
mathematicians had been immensely creative, but at times it had led to errors and absurdities. Intuition had to
be supplemented by careful analysis and logical proof. One reason was the increased complexity of the material
being studied. It was all very well, in the early stages, to explain that integration gave the area under a curve,
and everyone had an idea of what area meant. It is not the same when you are dealing with a perforated graph like
that of Riemann's f(x). Does it indeed determine an area? If so, we have to define exactly what is meant by that
area and how to measure it. This is characteristic of 19th century mathematical works. It is no longer felt that
everyday ideas are sufficient: we have to make sure that each concept is accurately defined, and that we proceed
logically from this definition when we use it.
This procedure can make mathematical textbooks resemble legal documents, which are rarely attractive reading. For
people who are interested in mathematics mainly for its applications, and indeed for mathematicians themselves,
it is important that the formal, rigorous treatment should be supplemented by a commentary explaining what it is
all about. If you are browsing through the mathematical shelves of a library, it is important to realise which
books are dedicated to both of these two tasks.
Does Rigour Contradict Common Sense?
Earlier we found it surprising that a series like (1) above, consisting entirely of continuous functions, could
have a sum, like F(x) in Figure 3, with breaks in it. Is this in fact
impossible, as our intuition tends to suggest?
The explanation lies in the meaning of the sum of an infinite series, about which early mathematicians were rather vague, and which was clarified in the 19th century. The objection would be perfectly valid if we were talking about the sum of a finite number of terms. However many terms of the series (1) you may take, its graph will always be free from breaks. But y in equation (1) is not equal to the sum of any finite number of terms; it is something that is approached more and more closely, but never reached as you take larger and larger numbers of terms.
The series for f(x) is
Figure 5 shows the graph for the sum of the first 10 terms of this series. It does not consist of straight lines nor does it have a break in it, but it is doing its best to resemble the graph of F(x) in Figure 4a.
The essential point is that we can find a continuous curve that approximates as closely as anybody may require
to a discontinuous curve, and as Figure 5 shows, this is something we can visualise. With the help of the rigorous
definition of the sum of an infinite series we are able to imagine something that even the geniuses of 1750 regarded
as impossible.
Warwick Sawyer retired from the University of Toronto in 1976. Previously he taught mathematics at university level
in Britain, New Zealand and the USA. From 1948 to 1950 he was the first Head of Mathematics at the University of
Ghana. He has written twelve books, including Mathematician's Delight and Prelude to Mathematics. Their aim is
to enable scientists, engineers and the general public to use any mathematics they might need, with understanding
and without anxiety.
This article first appeared in the November 1990 issue of Mathematical Review.
Copyright © W. W. Sawyer & Mark Alder 2001
Version: 22nd March 2001
|